sbi: simulation-based inference toolkit

sbi is a Python package for simulation-based inference, designed to meet the needs of both researchers and practitioners. Whether you need fine-grained control or an easy-to-use interface, sbi has you covered.

With sbi, you can perform parameter inference using Bayesian inference: Given a simulator that models a real-world process, SBI estimates the full posterior distribution over the simulator’s parameters based on observed data. This distribution indicates the most likely parameter values while additionally quantifying uncertainty and revealing potential interactions between parameters.

sbi provides access to simulation-based inference methods via a user-friendly interface:

import torch
from sbi.inference import NPE

# define shifted Gaussian simulator.
def simulator(θ): return θ + torch.randn_like(θ)
# draw parameters from Gaussian prior.
θ = torch.randn(1000, 2)
# simulate data
x = simulator(θ)

# choose sbi method and train
inference = NPE()
inference.append_simulations(θ, x).train()

# do inference given observed data
x_o = torch.ones(2)
posterior = inference.build_posterior()
samples = posterior.sample((1000,), x=x_o)

Overview

To get started, install the sbi package with:

pip install sbi

for more advanced install options, see our Install Guide.

Then, check out our material:

• Motivation and approach
  
  General motivation for the SBI framework and methods included in sbi.

• Tutorials and Examples
  
  Various examples illustrating how to
  get started or use the sbi package.

• Reference API
  
  The detailed description of the package classes and functions.

• Citation
  
  How to cite the sbi package.

Motivation and approach

Many areas of science and engineering make extensive use of complex, stochastic, numerical simulations to describe the structure and dynamics of the processes being investigated.

A key challenge in simulation-based science is constraining these simulation models’ parameters, which are interpretable quantities, with observational data. Bayesian inference provides a general and powerful framework to invert the simulators, i.e. describe the parameters that are consistent both with empirical data and prior knowledge.

In the case of simulators, a key quantity required for statistical inference, the likelihood of observed data given parameters, \(\mathcal{L}(\theta) = p(x_o|\theta)\), is typically intractable, rendering conventional statistical approaches inapplicable.

sbi implements powerful machine-learning methods that address this problem. Roughly, these algorithms can be categorized as:

• Neural Posterior Estimation (amortized NPE and sequential SNPE),
• Neural Likelihood Estimation ((S)NLE), and
• Neural Ratio Estimation ((S)NRE).

Depending on the characteristics of the problem, e.g. the dimensionalities of the parameter space and the observation space, one of the methods will be more suitable.

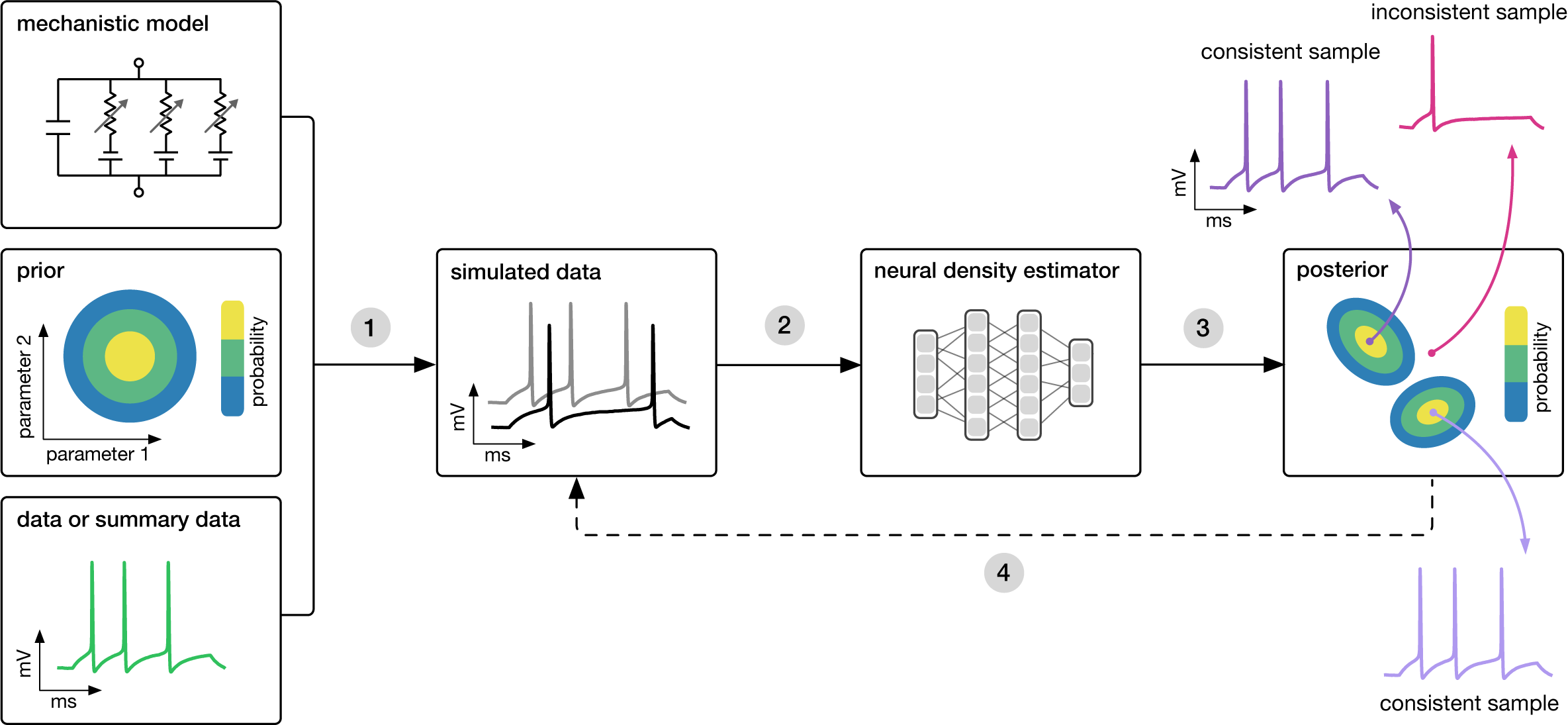
Goal: Algorithmically identify mechanistic models that are consistent with data.

Each of the methods above needs three inputs: A candidate mechanistic model, prior knowledge or constraints on model parameters, and observational data (or summary statistics thereof).

The methods then proceed by

1. sampling parameters from the prior followed by simulating synthetic data from these parameters,
2. learning the (probabilistic) association between data (or data features) and underlying parameters, i.e. to learn statistical inference from simulated data. How this association is learned differs between the above methods, but all use deep neural networks.
3. This learned neural network is then applied to empirical data to derive the full space of parameters consistent with the data and the prior, i.e. the posterior distribution. The posterior assigns high probability to parameters that are consistent with both the data and the prior, and low probability to inconsistent parameters. While NPE directly learns the posterior distribution, NLE and NRE need an extra MCMC sampling step to construct a posterior.
4. If needed, an initial estimate of the posterior can be used to adaptively generate additional informative simulations.

See Cranmer, Brehmer, Louppe (2020) for a recent review on simulation-based inference.

Implemented algorithms

sbi implements a variety of amortized and sequential SBI methods.

Amortized methods return a posterior that can be applied to many different observations without retraining (e.g., NPE), whereas sequential methods focus the inference on one particular observation to be more simulation-efficient (e.g., SNPE).

Below, we list all implemented methods and the corresponding publications. To see how to access these methods in sbi, check out our Inference API’s reference and the tutorial on implemented methods.

Posterior estimation ((S)NPE)

• Fast ε-free Inference of Simulation Models with Bayesian Conditional Density Estimation
  by Papamakarios & Murray (NeurIPS 2016)
  [PDF] [BibTeX]

• Flexible statistical inference for mechanistic models of neural dynamics
  by Lueckmann, Goncalves, Bassetto, Öcal, Nonnenmacher & Macke (NeurIPS 2017)
  [PDF] [BibTeX]

• Automatic posterior transformation for likelihood-free inference
  by Greenberg, Nonnenmacher & Macke (ICML 2019)
  [PDF] [BibTeX]

• BayesFlow: Learning complex stochastic models with invertible neural networks
  by Radev, S. T., Mertens, U. K., Voss, A., Ardizzone, L., & Köthe, U. (IEEE transactions on neural networks and learning systems 2020)
  [Paper]

• Truncated proposals for scalable and hassle-free simulation-based inference
  by Deistler, Goncalves & Macke (NeurIPS 2022)
  [Paper]

• Flow matching for scalable simulation-based inference
  by Dax, M., Wildberger, J., Buchholz, S., Green, S. R., Macke, J. H., & Schölkopf, B. (NeurIPS, 2023)
  [Paper]

• Compositional Score Modeling for Simulation-Based Inference
  by Geffner, T., Papamakarios, G., & Mnih, A. (ICML 2023)
  [Paper]

Likelihood-estimation ((S)NLE)

• Sequential neural likelihood: Fast likelihood-free inference with autoregressive flows
  by Papamakarios, Sterratt & Murray (AISTATS 2019)
  [PDF] [BibTeX]

• Variational methods for simulation-based inference
  by Glöckler, Deistler, Macke (ICLR 2022)
  [Paper]

• Flexible and efficient simulation-based inference for models of decision-making
  by Boelts, Lueckmann, Gao, Macke (Elife 2022)
  [Paper]

Likelihood-ratio-estimation ((S)NRE)

• Likelihood-free MCMC with Amortized Approximate Likelihood Ratios
  by Hermans, Begy & Louppe (ICML 2020)
  [PDF]

• On Contrastive Learning for Likelihood-free Inference
  by Durkan, Murray & Papamakarios (ICML 2020)
  [PDF]

• Towards Reliable Simulation-Based Inference with Balanced Neural Ratio Estimation
  by Delaunoy, Hermans, Rozet, Wehenkel & Louppe (NeurIPS 2022)
  [PDF]

• Contrastive Neural Ratio Estimation
  by Benjamin Kurt Miller, Christoph Weniger & Patrick Forré (NeurIPS 2022)
  [PDF]

Diagnostics

• Simulation-based calibration
  by Talts, Betancourt, Simpson, Vehtari, Gelman (arxiv 2018)
  [Paper]

• Expected coverage (sample-based)
  as computed in Deistler, Goncalves, & Macke (NeurIPS 2022)
  [Paper] and in Rozet & Louppe [Paper]

• Local C2ST
  by Linhart, Gramfort & Rodrigues (NeurIPS 2023)
  [Paper]

• TARP
  by Lemos, Coogan, Hezaveh & Perreault-Levasseur (ICML 2023)
  [Paper]