sbi: simulation-based inference

sbi: A Python toolbox for simulation-based inference.

Inference can be run in a single line of code

posterior = infer(simulator, prior, method='SNPE', num_simulations=1000)

or in a few lines for more flexibility:

inference = SNPE(prior=prior)
_ = inference.append_simulations(theta, x).train()
posterior = inference.build_posterior()

sbi lets you choose from a variety of amortized and sequential SBI methods:

Amortized methods return a posterior that can be applied to many different observations without retraining, whereas sequential methods focus the inference on one particular observation to be more simulation-efficient. For an overview of implemented methods see below, or checkout or GitHub page.

Overview

• To learn about the general motivation behind simulation-based inference, and the inference methods included in sbi, read on below.

• For example applications to canonical problems in neuroscience, browse the recent research article Training deep neural density estimators to identify mechanistic models of neural dynamics.

• If you want to get started using sbi on your own problem, jump to installation and then check out the tutorial.

Motivation and approach

Many areas of science and engineering make extensive use of complex, stochastic, numerical simulations to describe the structure and dynamics of the processes being investigated.

A key challenge in simulation-based science is constraining these simulation models’ parameters, which are intepretable quantities, with observational data. Bayesian inference provides a general and powerful framework to invert the simulators, i.e. describe the parameters which are consistent both with empirical data and prior knowledge.

In the case of simulators, a key quantity required for statistical inference, the likelihood of observed data given parameters, \(\mathcal{L}(\theta) = p(x_o|\theta)\), is typically intractable, rendering conventional statistical approaches inapplicable.

sbi implements powerful machine-learning methods that address this problem. Roughly, these algorithms can be categorized as:

• Neural Posterior Estimation (amortized NPE and sequential SNPE),
• Neural Likelihood Estimation ((S)NLE), and
• Neural Ratio Estimation ((S)NRE).

Depending on the characteristics of the problem, e.g. the dimensionalities of the parameter space and the observation space, one of the methods will be more suitable.

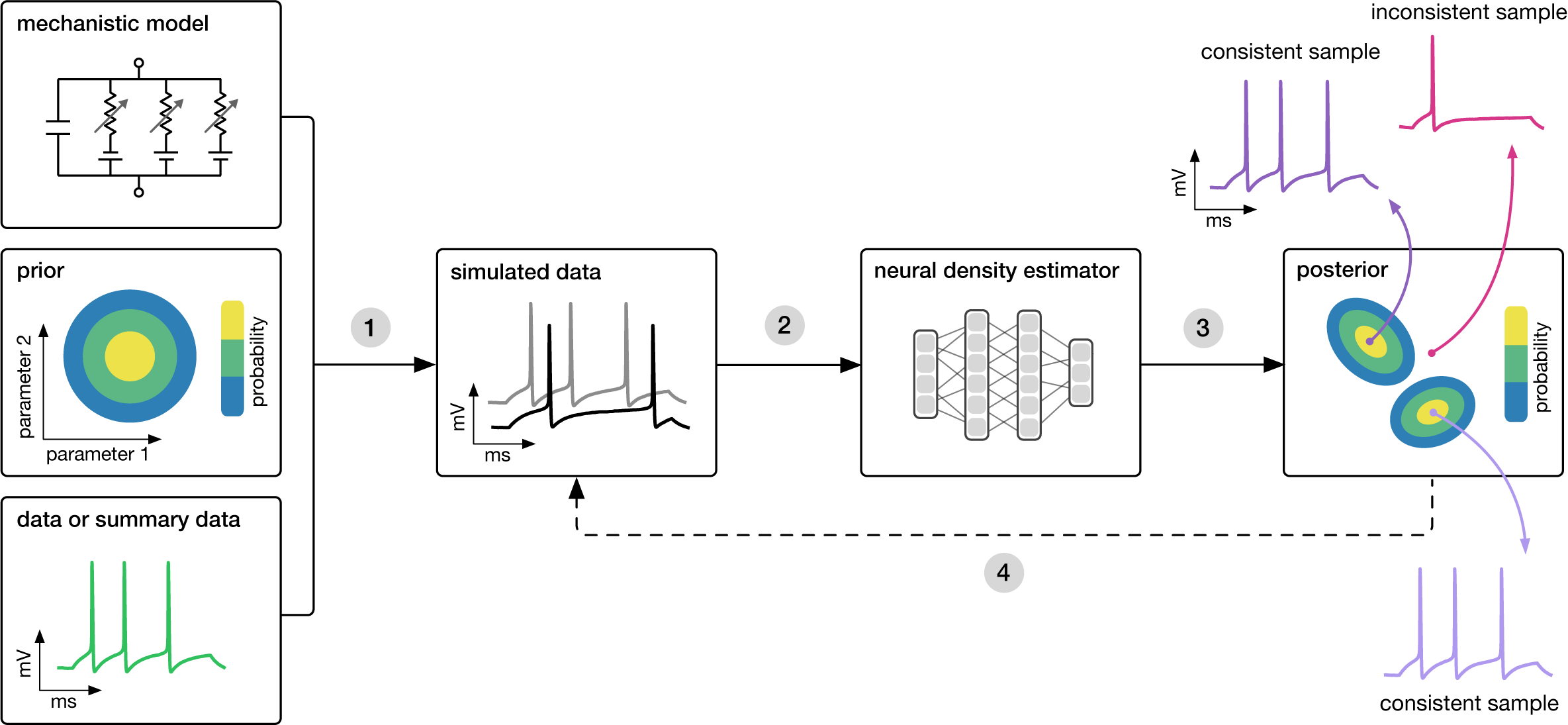
Goal: Algorithmically identify mechanistic models which are consistent with data.

Each of the methods above needs three inputs: A candidate mechanistic model, prior knowledge or constraints on model parameters, and observational data (or summary statistics thereof).

The methods then proceed by

1. sampling parameters from the prior followed by simulating synthetic data from these parameters,
2. learning the (probabilistic) association between data (or data features) and underlying parameters, i.e. to learn statistical inference from simulated data. The way in which this association is learned differs between the above methods, but all use deep neural networks.
3. This learned neural network is then applied to empirical data to derive the full space of parameters consistent with the data and the prior, i.e. the posterior distribution. High posterior probability is assigned to parameters which are consistent with both the data and the prior, low probability to inconsistent parameters. While SNPE directly learns the posterior distribution, SNLE and SNRE need an extra MCMC sampling step to construct a posterior.
4. If needed, an initial estimate of the posterior can be used to adaptively generate additional informative simulations.

Publications

See Cranmer, Brehmer, Louppe (2020) for a recent review on simulation-based inference.

The following papers offer additional details on the inference methods implemented in sbi. You can find a tutorial on how to run each of these methods here.

Posterior estimation ((S)NPE)

• Fast ε-free Inference of Simulation Models with Bayesian Conditional Density Estimation
  by Papamakarios & Murray (NeurIPS 2016)
  [PDF] [BibTeX]

• Flexible statistical inference for mechanistic models of neural dynamics
  by Lueckmann, Goncalves, Bassetto, Öcal, Nonnenmacher & Macke (NeurIPS 2017)
  [PDF] [BibTeX]

• Automatic posterior transformation for likelihood-free inference
  by Greenberg, Nonnenmacher & Macke (ICML 2019)
  [PDF] [BibTeX]

• Truncated proposals for scalable and hassle-free simulation-based inference
  by Deistler, Goncalves & Macke (NeurIPS 2022)
  [Paper]

Likelihood-estimation ((S)NLE)

• Sequential neural likelihood: Fast likelihood-free inference with autoregressive flows
  by Papamakarios, Sterratt & Murray (AISTATS 2019)
  [PDF] [BibTeX]

• Variational methods for simulation-based inference
  by Glöckler, Deistler, Macke (ICLR 2022)
  [Paper]

• Flexible and efficient simulation-based inference for models of decision-making
  by Boelts, Lueckmann, Gao, Macke (Elife 2022)
  [Paper]

Likelihood-ratio-estimation ((S)NRE)

• Likelihood-free MCMC with Amortized Approximate Likelihood Ratios
  by Hermans, Begy & Louppe (ICML 2020)
  [PDF]

• On Contrastive Learning for Likelihood-free Inference
  Durkan, Murray & Papamakarios (ICML 2020)
  [PDF]

• Towards Reliable Simulation-Based Inference with Balanced Neural Ratio Estimation
  by Delaunoy, Hermans, Rozet, Wehenkel & Louppe (NeurIPS 2022)
  [PDF]

• Contrastive Neural Ratio Estimation
  Benjamin Kurt Miller, Christoph Weniger, Patrick Forré (NeurIPS 2022)
  [PDF]

Utilities

• Restriction estimator
  by Deistler, Macke & Goncalves (PNAS 2022)
  [Paper]

• Simulation-based calibration
  by Talts, Betancourt, Simpson, Vehtari, Gelman (arxiv 2018)
  [Paper])

• Expected coverage (sample-based)
  as computed in Deistler, Goncalves, Macke [Paper] and in Rozet, Louppe [Paper]